§3.6 最小值与最大值问题

一、闭区间上连续函数的最值

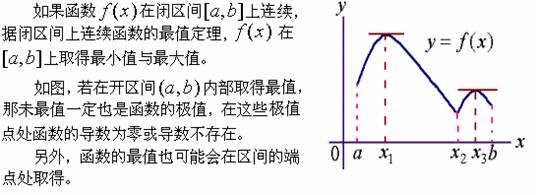
综上讨论，函数取得最值的点只能是区间的端点或开区间内导数为零、导数不存在的点。计算函数在这些点处的函数值，比较它们的大小就可得到函数的最值。

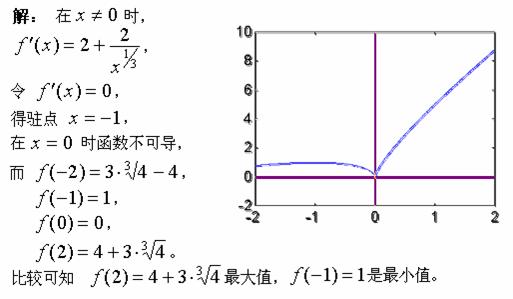
【例1】求函数在上的最值。

二、非闭区间上定义的函数最值

对于非闭区间上定义的函数，它有可能存在着最值，也有可能不存在着最值，这就给求函数最值带来了困难。

探讨函数最值，可先求函数的可疑极值点(驻点，导数不存在的点)，并讨论由这些点所形成的区间上函数的单调性，再利用函数的性态来判断函数在这些可疑点处是否有最值。

下面以例子来说明具体求法。

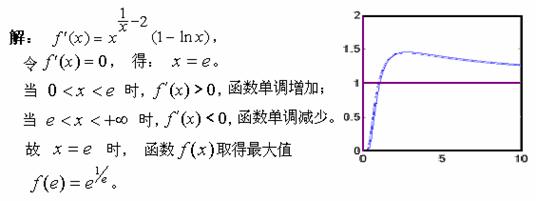
【例2】求函数 在定义区间 上的最值。

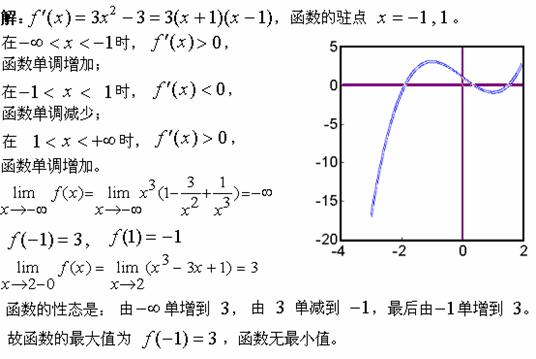
【例3】求函数在 的最值。

三、实用最值应用问题

利用求函数的最值来处理实际问题，有如下几个步骤：

1、据实际问题列出函数表达式及它的定义区间；

2、求出该函数在定义区间上的可能极值点(驻点和一阶导数不存在的点)；

3、讨论函数的单调性，确定函数在可能极值点处是否取得最值。

【例4】试求单位球的内接圆锥体体积最大者的高，并求此体积的最大值。

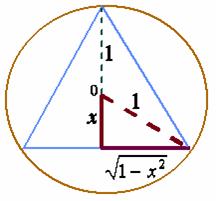
解：设球心到锥底面的垂线长为，则圆锥的高为，圆锥面底面半径为，圆锥体积为

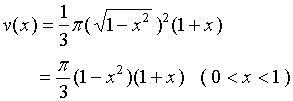
由 ,得驻点，

在上，，函数单增；

在上，，函数单减，

故是函数的最大值点，是函数的最大值。

于是最大的体积为，此时的高为。